Weekly Notes for Week 22
This week we finish discussing cycles/rings and I will present i) an applications of MCB in chemistry and ii) show “alternative” ring sets as have been used in chemistry literature. We will discuss various ring/cycle sets and compare wrt. uniqueness, size, and other properties. Before describing a more unknown cycle invariant from the paper be Berger, Gritzmann, and de Vries based on MCB, I will show another (much simpler and much more prominent) graph invariant: the Wiener Index. For the Wiener Index I will show an application example of how to predict the boiling point of paraffins.
- Mandatory Reading (same as for week 21):
- Franziska Berger, Christoph Flamm, Petra M. Gleiss, Josef Leydold, Peter F. Stadler: Counterexamples in Chemical Ring Perception. Journal of Chemical Information and Modeling 44(2): 323-331 (2004)
- (Applications of MCB): Minimum Cycle Bases and Their Applications, Franziska Berger, Peter Gritzmann, and Sven de Vries - only section 3.2 is mandatory
Exercises 05 (in class, no submission):
1.) Cyles/ Rings :
Complete the following table
| Ring Set | Unique | Contains Basis | Contains MCB | Contains all Relevant Cycles | Size |
|---|---|---|---|---|---|
| SSSR/MCB | Yes | ||||
| Faces(G) | |||||
| Elementary Cycles | |||||
| Relevant Cycles | |||||
| ESSR |
2.) Cycle Invariant
Determine the cycle invariant as described in the article Minimum Cycle Bases and Their Applications, Franziska Berger, Peter Gritzmann, and Sven de Vries for the following molecules:
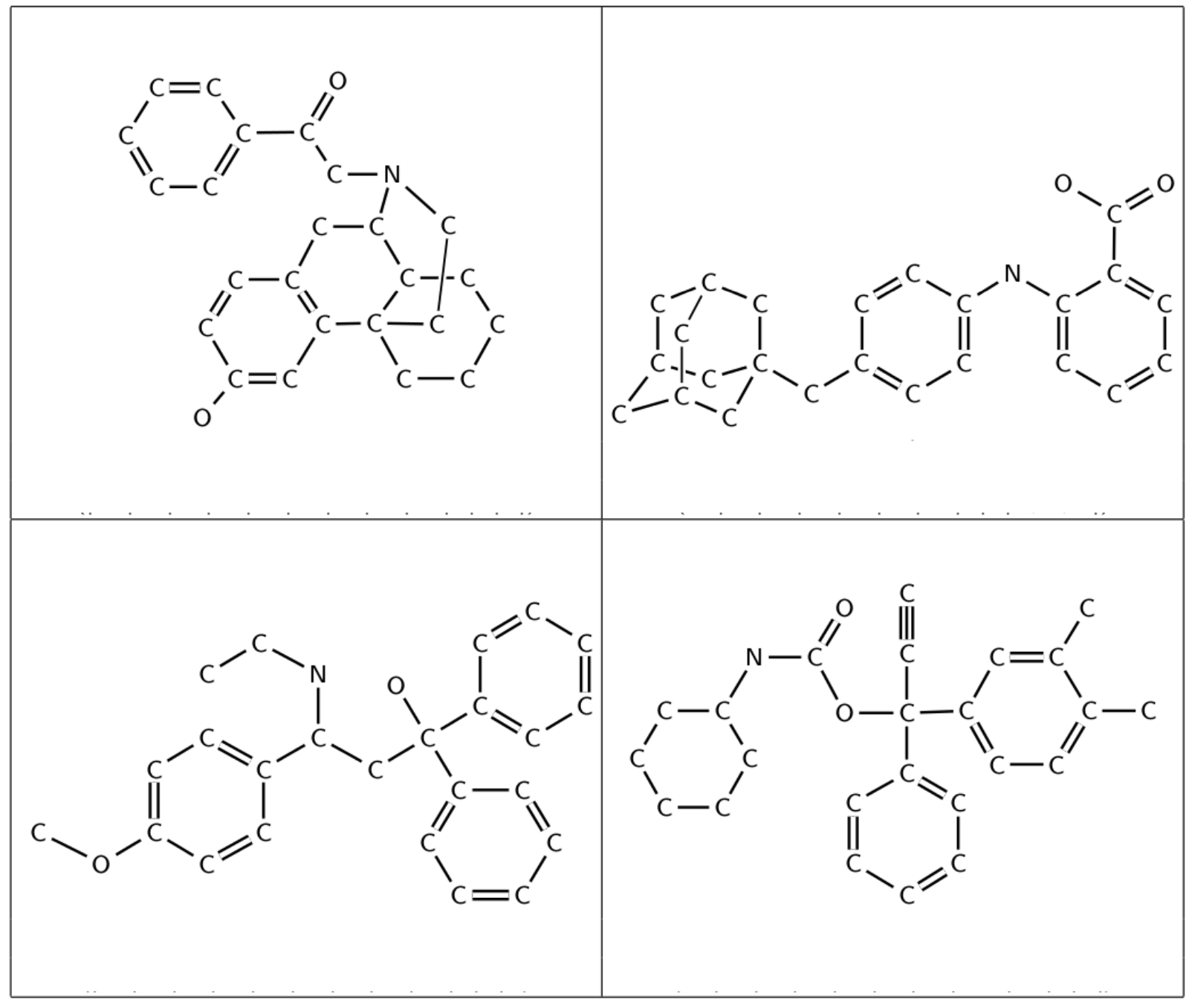
3.) Wiener Index
Given the following graph G representing the chemical compound 2,3-dimethylpentan:
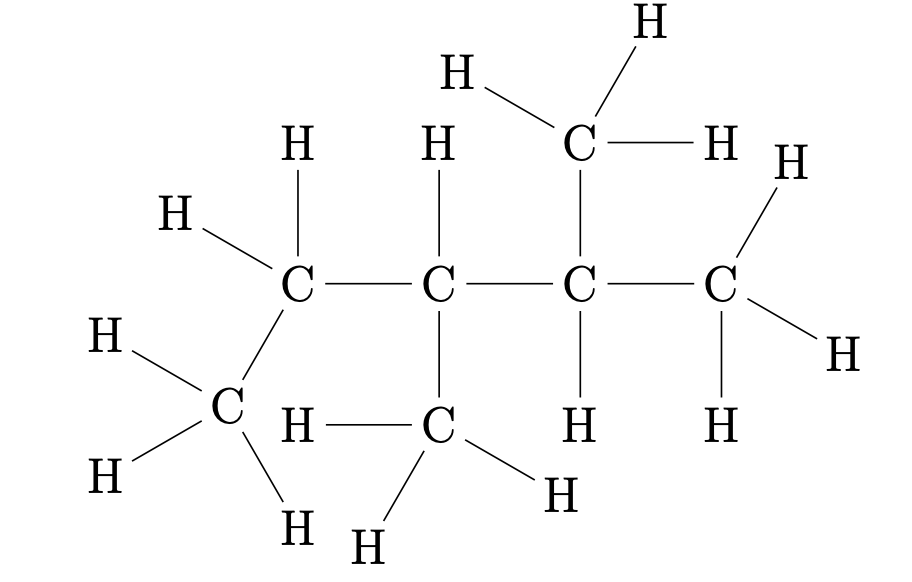
- Determine the edge-weight matrix of the graph of the carbon backbone.
- Determine the distance matrix.
- Determine the Wiener-Index.
- Determine the number of shortest paths of length 3.
- Determine the value p0 and w0 of the formula for predicting the boiling point for this compound.
- Determine the estimated boiling points and compare it to the real boiling point.
- What is the asymptotic worst case performance for finding the distance matrix based on repeated squaring?
- Do you know a method that has a better asymptotic worst case perfor- mance?